ゲストさん
計算コラム
(87) 数値積分
2017/9/12
| ある関数を積分するとき、積分した結果を式で表せるもの、つまり解析的に積分できるものは限られている。
そのような中で、関数の定積分の値を数値的に求める手法として「数値積分法」がある。
数値積分法には様々な手法があり、簡単なもので「台形則」、少し複雑な方法で「Gauss求積法」等が挙げられる。
「台形則」は定積分を台形の集まりとして計算する。（図1）
簡単に計算できる方法なので用いられることも多いが、分割数を増やしても、精度はそれほど期待できない。
これに対して、Gauss求積法は定積分をある点「分点」での「重み」と、その分点での関数の値を足し合わせることによって計算される。（式2） Gauss求積法は条件により制限はあるが、少ない演算でもかなりの精度で求めることが可能である。 例えば、(式3)を台形則で積分すると、8分割～64分割で求めても3,4桁の精度しか出ないのに対し、Gauss-Legendre則で積分すると、下記のように8分割でも11桁、64分割では50桁の精度で求められる。
「数値積分」計算を整理・充実したので、是非利用して数値積分の世界に触れてみて欲しい。 |  |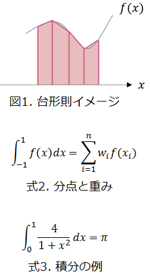
| 関連リンク | |
| [1] 台形則 [2] ガウス-ルジャンドル数値積分 | |
 |
ブックマーク
実行履歴
計算コラム 