計算コラム

  1. ホーム/
  2. 計算コラム

(58) 5種類だけの正多面体

  • Back
2013/2/20
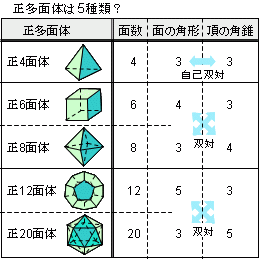
同一の正多角形からなる凸の多面体は5種類しか存在しない。正12面体と正20面体を発見し5種類以外存在しないことを証明したのは古代ギリシャのピタゴラス学派だそうだ。だが、遡る石器時代のスコットランドで正多面体の石玉が見つかっている。きっとその形状の美しさに惹かれて作ったのだろう。さて正6面体の頂点を面に、面心を頂点に入れ替えると正8面体に変身する。逆も然りで相互に双対の多面体となる。正12面体と正20面体も双対関係となる。正4面体だけが面と頂点を入れ替えても同じ正4面体で変身しない。この意味から、正多面体は3種類とも言えるのでは。
関連リンク
[1]正多面体の体積
[2] Neolithic Carved Stone Polyhedra

ブックマーク

実行履歴

計算コラム