計算コラム
(45) ピタゴラス定理の証明
2011/12/01
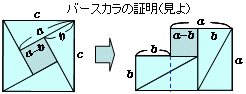
| 直角三角形の3辺a,b,cはa2+b2=c2が成り立つ。中学校で習う周知のピタゴラス定理だ。3辺が3:4:5の比は直角三角形になることを知っていた古代のエジプト人は、12等分した紐から直角を作り出していた。さてこの定理の証明法は200以上あると言われる。ユークリッドの正統な証明は多くの補助線を使っており、学ぶと数学嫌いになるらしい。インドの数学者バースカラ2世の証明は解り易い。タイル移動の図に、ただ「見よ」が書かれおり、一目瞭然で理解できる。アインシュタインの証明も秀逸だ。直角三角形に垂線を引き相似関係から導いている。時空の相対性を発見した洞察力がこの証明にも生きているようだ。新しい証明にトライしてみよう。 | 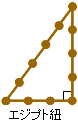 |
| 関連リンク | |
| [1]ピタゴラスの定理 [2]直角三角形 | |
 | |
 | |
 |


 ゲストさん
ゲストさん



 ブックマーク
ブックマーク 実行履歴
実行履歴 計算コラム
計算コラム 