インド式2乗(下1桁が5の数)
下1桁が5の数値の2乗を簡単に計算できます。インド式暗算で脳を鍛えましょう。 | ||
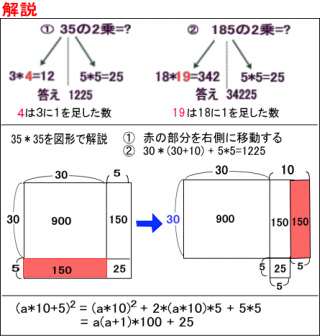 |
| ・この手法は 1の位が「5」でなくとも足して「10」になり、10の位が同じ数字なら適用できます。 例)73×77=5621 |
- 使用目的
- 心の安らぎ
- ご意見・ご感想
- 目からウロコ
数字って面白いね
[1] 2024/03/30 23:03 60歳以上 / 会社員・公務員 / 非常に役に立った /
- 使用目的
- 資格試験
- ご意見・ご感想
- 乗数の検索でこのサイトにきました。
5の倍数だけと使用範囲が限定され過ぎててあまり役に立たない感想
[2] 2022/10/15 08:32 40歳代 / その他 / 役に立たなかった /
- 使用目的
- 趣味
- ご意見・ご感想
- 分かりやすい
[3] 2021/01/17 01:51 20歳未満 / 小・中学生 / 役に立った /
- 使用目的
- 役に立たない。
- ご意見・ご感想
- インド式計算法は愚者の計算法である。
ほとんどが中学で習う展開公式の応用に過ぎないので展開公式を理解していればほぼ無用。
暗算で解けと言っているが、実際には計算途中の数字は憶えていられないからメモを取る必要があり、記憶力に優れていないと完全な暗算では解けない。
なお、このページの5の倍数の二乗だったら2桁なら2倍して二乗して4で割る方が速い。
45^2=90^2/4=8100/4=2025
または5で割って二乗して100倍して4で割っても良い。
185^2=37^2*100/4=(30+7)^2*100/4=(30^2+30*14+7^2)*100/4=1369*100/4=34225
更に、下一桁の和が10になる場合は展開公式の応用で足りる。というか、展開公式を応用すれば下一桁の和が10にならなくても問題ない。
73*77=(70+3)(70+7)=4900+700+21=5621
77^2=(80-3)^2=6400-480+9=5929
※77^2=7^2*11^2=49*121=(50-1)*121=6050-121=5929という方法もある。
74*78=(70+4)(70+8)=4900+840+32=5772
[4] 2016/06/15 05:20 40歳代 / 自営業 / 役に立たなかった /
- 使用目的
- 順次勉強したい
- ご意見・ご感想
- 図形での解説が有難い
[5] 2013/04/10 22:45 60歳以上 / 自営業 / 役に立った /
- 使用目的
- 暗算のコツとして覚えておきたい。
[6] 2011/08/23 04:51 50歳代 / 会社員・公務員 / 役に立った /
- 使用目的
- 脳の活性
- ご意見・ご感想
- 問題の全体から答えが出せる様になりましたよ
[7] 2010/04/08 01:48 60歳以上 / 無職 / 役に立った /
- 使用目的
- 脳のトレーニング
- ご意見・ご感想
- もっといろんな問題に挑戦したいです。
[8] 2009/12/02 03:25 60歳以上 / 無職 / 役に立った /
- 使用目的
- 頭の体操
- ご意見・ご感想
- 計算の仕組みを分解して考える面白さを発見
[9] 2009/11/03 13:55 60歳以上 / 無職 / 役に立った /
- 使用目的
- 孫にやって見せておじいちゃんを尊敬させる。呵呵。 米寿のGG.
- ご意見・ご感想
- 今朝(2009,11,3)のTBSラジオで紹介されたので早速、KEISANにアクセス。面白い。感謝、感謝
[10] 2009/11/03 02:28 60歳以上 / 無職 / 役に立った /
- 【インド式2乗(下1桁が5の数) にリンクを張る方法】


 ゲストさん
ゲストさん








 ブックマーク
ブックマーク

 実行履歴
実行履歴