計算例

  1. ホーム/
  2. 計算例

フリー計算での入力(実数) ・・・「実数DEG」を選択

例題計算内容 計算式入力 [計算] → 答え桁数モード
四則演算10+20-30*4/6 [計算] → 106
べき乗計算3*4^2 [計算] → 486
指数計算99*1.23E+3 [計算] → 1217706
関数を使用sqrt(4) [計算] → 26
変数を使用sin(x) [計算]
(変数 x) 456 → 0.994522		6実数DEG
桁数の変更cos(12345) [計算] → -0.258819
[桁数] 22桁 [計算] → -0.2588190451025207623489		6
↓
22		実数DEG
角度を変更cos(123456) [計算] → 0.9135454576426008955021
[モード] RAD [計算] → -0.67229488165658452		22↓
実数RAD
繰返計算sin(x) [計算]
(変数 x ) 1, 0.1, 10 [計算] →
1 0.8414709848078965066525
1.1 0.8912073600614353399518
1.2 0.9320390859672263496701
・・・
1.9 0.9463000876874144884897		22実数RAD

このページの先頭へ

フリー計算での入力（複素数）・・・「複素数RAD」を選択

例題計算内容
計算式入力 [計算] → 答え		桁数モード
四則演算 (3+4i)*(5+6i) [計算] → -9 +38i 6 複素数RAD
ルート計算 sqrt(i)[計算] → 0.707107 +0.707107i 6 複素数RAD

このページの先頭へ

フリー計算でのグラフ作成

例題
式と変数		 モード グラフ描画と設定
ルート √

sqrt(x)
x= 0,0.1,51		 6桁
実数DEG
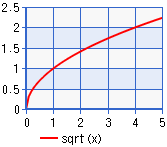シート幅=190, 高さ=170,
X軸ｽｷｯﾌﾟ=10
三角関数

sin(x);cos(x)
x= 0,5,101		 6桁
実数DEG
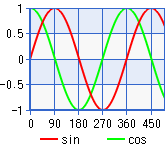シート幅=200, 高さ=170,
Y軸目盛り Max=1, Min=-1
X軸ｽｷｯﾌﾟ=18,
凡例位置 下, 高さ10
正規分布

normalpd(x)
x=-4,0.1,81		 6桁
実数DEG
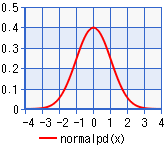シート幅=190, 高さ=170,
Y軸目盛り Max=0.5, Min=0
X軸目盛り 10plot毎
凡例位置 下, 高さ10
ベッセル関数
J0(x),Y0(x)

besselj(0,x);
bessely(0,x)
x= 0,0.1,101		 6桁
実数DEG
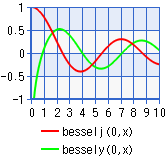シート幅=190, 高さ=180,
Y軸目盛り Max=1, Min=-1
凡例位置 下, 高さ30, 行数2

精度計算 (桁数可変技術の応用で精度保証計算を追求)

例題 モード Keisan (6桁演算) 精度保証
Excel2003 (16桁演算)
小数計算
0.4-0.3-0.1		 6桁
実数RAD		 0.4-0.3-0.1 =0
(0.4-0.3-0.1) =2.77556E-17
2進10進変換で誤差発生
π計算
sin(9π)		 6桁
実数RAD		 sin(9*pi) =0
SIN(9*PI()) =1.10263E-15
πの有限数値化で誤差発生
無理数計算
9√2-√162		 6桁
実数RAD		 9*sqrt(2)-sqrt(162) =0
(9*SQRT(2)-SQRT(162)) =1.77636E-15
無理数の有限数値化で誤差発生
複素数計算
(1+i)4		 6桁
複素数RAD		 (1+i)^4 =-4
IMPOWER("1+i", 4) =-4 +4.89842541528951E-16i
解 (1+i)4 =(√2*eiπ/4)4
　　　　　=(√2)4*eiπ =-4
√(1+x)-1
x=1.23456E-100		 6桁
実数RAD		 sqrt(1+ 1.23456E-100)-1 =6.1728E-101
SQRT(1+ 1.23456E-100)-1 =0
x≪1の場合、1+x=1となり精度出ない
eln(1+x)-1
x=1.23456E-14		 6桁
実数RAD		 e^ln(1+ 1.23456E-14)-1 =1.23456E-14
EXP(LN(1+ 1.23456E-14))-1 =1.24345E-14
x≒1E-14の場合、3桁しか精度出ない
eln(1+x)-1
x=1.23456E-15		 6桁
実数RAD		 e^ln(1+ 1.23456E-15)-1 =1.23456E-15
EXP(LN(1+ 1.23456E-15))-1 =0
x<1E-15の場合、全く精度出ない
人間の運動エネルギー
E=mc2(1-√(1-v2/c2))
m= 80kg
v= 100/9.77m/s
c= 299792458m/s		 6桁
実数RAD		 m=80;v=100/9.77;c=299792458;
m*c^2*(1-sqrt(1-v^2/c^2)) =4190.55
m=80;v=100/9.77;c=299792458;
m*c^2*(1-SQRT(1-v^2/c^2)) =3991.274772
v≪cの場合、ﾆｭｰﾄﾝ近似で E=mv2/2=4190.55