【最も遠くに飛ぶのは45°ではない?】飛距離を最大にする角度    実行数: 24057

  1. ホーム
  2.  / みんなの自作式（科学）
  3.  / 物理（一般）

物体の地面からの高さhと、物体を打ち出す速度v0から、飛距離が最も大きくなる最適打出角度θ0、最大の飛距離lmaxなどを求めます。

どんな条件でも水平面に対して45°の角度で投げれば最も飛距離が出せると思っていませんか？
確かに、地上0ｍの地点から投げた場合は、45°で投げると最も遠くに飛びます。
しかし、人間が投げる場合は身長と手の長さがあるので、地上2ｍほどの地点から投射が始まります。
このように投げ出しの位置が地面より高い場合、45°では最も遠くに飛びません。
例えば、2mの高さから砲丸を10m/sで投げる場合、計算上40.28°が最も飛距離が最大になります。(数式の下の図を参照)
また、飛距離が最大になるとき、次の関係式が必ず成り立ちます、
・最適打出角度θ0＋着地角度θe＝90°
・tan(最適打出角度θ0)＝打出速度v0 / 着地速度ve

※空気抵抗は無視しています。
※打出地点より到達地点が高い場合は、打出地点の高さはマイナスにします。
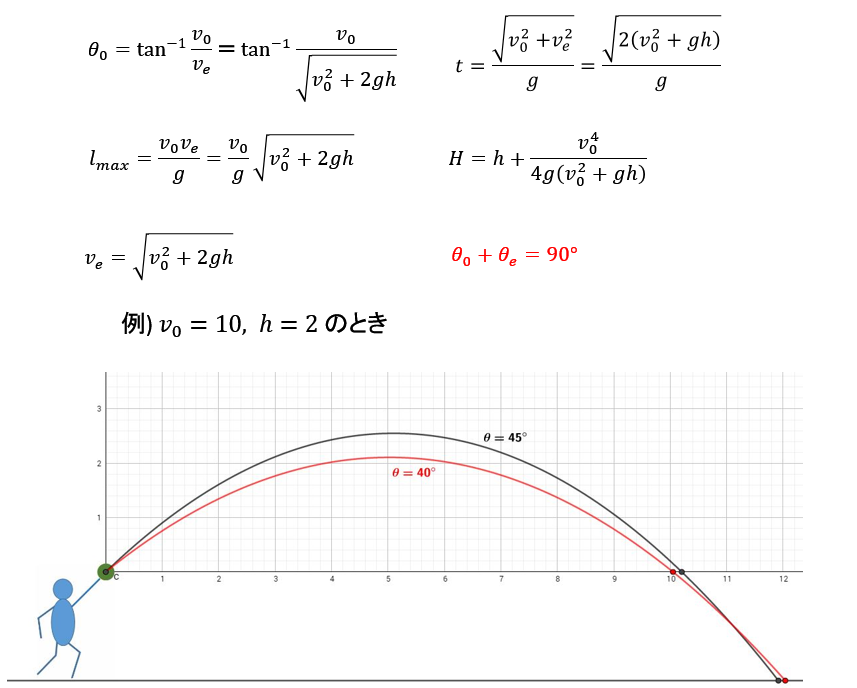【最も遠くに飛ぶのは45°ではない?】飛距離を最大にする角度
打出速度 v0
    2. m/s
    3. ※時速のときは3.6で割ってください
投出しの高さ h
    2. m
    3. ※人が投げる場合は手の高さ
[重力加速度 g
    2. m/s^2]
最適打出角度 θ0
    1.  
    2. °
最大飛距離 lmax
    1.  
    2. m
滞空時間 t
    1.  
    2. 秒
到達高度 H
    1.  
    2. m
着地速度 ve
    1.  
    2. m/s
=
    1.  
    2. km/h
着地角度 θe
    1.  
    2. °
最適打出角度+着地角度 θ0+θe
    1.  
    2. °
【最も遠くに飛ぶのは45°ではない?】飛距離を最大にする角度
★砲丸投げの場合、実際の打出角度は45°よりも小さいことが多いです。
一つの理由として、前述したとおり投げ出しの位置が地面より高い場合、飛距離が最大になる角度は45°より小さいからです。二つ目の理由として、小さい角の方が力が伝わりやすく砲丸を効率よく加速し、初速度を大きくできるということがあげられるからです。

参考文献: 数研出版 改訂版 物理基礎　p37 コラム
本ライブラリは会員の方が作成した作品です。 内容について当サイトは一切関知しません。
    【最も遠くに飛ぶのは45°ではない?】飛距離を最大にする角度
    [1-1] /1件表示件数
    BACK NEXT
    [1]  2020/05/07 13:20   40歳代 / エンジニア / 非常に役に立った /
    使用目的
    あんな物やこんな物をとばすとどうなるか気になったので。
    ご意見・ご感想
    とってもためになりました！

    BACK NEXT

    アンケートにご協力頂き有り難うございました。

    送信を完了しました。



    Back

    【 【最も遠くに飛ぶのは45°ではない?】飛距離を最大にする角度 】のアンケート記入欄
    年齢
    職業

    この計算式は

    使用目的
    ご意見・ご感想・ご要望（バグ報告はこちら) バグに関する報告 (ご意見・ご感想・ご要望はこちら）
    計算バグ(入力値と間違ってる結果、正しい結果、参考資料など)
    説明バグ(間違ってる説明文と正しい説明文など)
    アンケートは下記にお客様の声として掲載させていただくことがあります。
    送信

    ブックマーク

    実行履歴